Blog

Quando un meteoroide giunge in prossimità della Terra inizia ad interagire con l’atmosfera, dando origine a quell’insieme di fenomeni luminosi e, a volte anche acustici, chiamati con il nome di meteora. La maggior parte dei meteoroidi si trasforma in meteore ad altezze in cui il cammino libero medio delle molecole d’aria varia da circa 0.1 metri (ad un’altezza di 90 km) a circa 1 metro (120 km). Tenendo presente che le dimensioni comuni dei meteoroidi sono dell’ordine di qualche millimetro, si deduce che il processo dominante durante il passaggio in atmosfera è l’impatto delle singole molecole d’aria contro il corpo cosmico.

Per l’attrazione gravitazionale della Terra, la velocità minima con cui un meteoroide entra nell’atmosfera terrestre è di circa 12 km/s mentre la velocità massima dipende dall’origine del corpo e dalla direzione del suo moto. Essa, perciò, risulta essere di circa 72 km/s, come somma della velocità della Terra attorno al Sole (29.7 km/s) e della velocità di fuga di una particella dal Sistema Solare in prossimità della Terra (42.1 km/s). Inoltre, il Sistema Solare non è un sistema isolato ma può essere attraversato da particelle ancora più veloci (granuli interstellari) provenienti dallo spazio interstellare, che si muovono a velocità fino ad oltre 200 km/s.

Un parametro importante è dato dalle dimensioni del meteoroide, che determina l’evoluzione del suo tragitto nell’atmosfera terrestre. Infatti, i meteoroidi più minuti, oggetti con masse inferiori ai 10^-9 kg tipiche dei cosiddetti micrometeoroidi, sono rallentati in modo che la caduta sia soggetta unicamente alla forza di gravità, senza alcuna emissione di radiazione. Per i meteoroidi di massa superiore invece l’interazione con gli strati più densi dell’atmosfera genera un’onda d’urto dovuta al fatto che tali oggetti cosmici si muovono a velocità ipersoniche. Le caratteristiche principali di quest’onda d’urto sono:

1. fronte dell’onda d’urto: è uno strato piuttosto sottile caratterizzato da brusche variazioni di pressione, densità e temperatura. In questo strato l’energia cinetica delle molecole in collisione viene convertita in eccitazione degli elettroni, dissociazione molecolare e ionizzazione di atomi;
2. strato compresso: è una regione di flusso non viscoso posto dietro al fronte d’onda dove il gas è, in prima approssimazione, in equilibrio termodinamico;
3. strato limite: è un sottile strato viscoso vicino al meteoroide in cui la componente tangenziale della velocità tende a decrescere fino ad annullarsi sulla superficie del corpo stesso. La struttura di questo strato diventa piuttosto complessa quando le molecole del meteoroide si vaporizzano, poiché si vengono a creare molteplici strati limite: uno per le molecole evaporate, uno strato limite aerodinamico in cui viene compensata la componente tangenziale della velocità e uno strato di equilibrio termico in cui la temperatura del gas e del meteoroide si uguagliano;
4. zona di stagnazione: è una regione posta dietro al meteoroide contenente  un gas rarefatto costituito da molecole evaporate dal meteoroide, da particelle espulse dalle disomogeneità del corpo durante la rotazione, etc.;
5. traccia meteorica: si forma come risultato del collasso dei gas che fluiscono attorno al corpo e della loro successiva diffusione.

Elementi principali dell’onda d’urto: 1. fronte d’onda; 2. strato compresso; 3. strato limite; 4. zona di stagnazione; 5. scia.

La semplice teoria fisica che descrive l’evolversi di un meteoroide interagente con l’atmosfera a velocità ipersoniche, può essere discussa richiamando le equazioni fondamentali che governano i processi di decelerazione, perdita di massa, luminosità e ionizzazione e assumendo che i coefficienti di frenamento, trasporto del calore, luminosità e ionizzazione presenti nelle equazioni stesse siano costanti.

La prima equazione fondamentale della teoria, l’equazione di decelerazione,  tiene conto dell’effetto frenante dell’atmosfera terrestre e si basa sull’ipotesi che la perdita della quantità di moto Mdv da parte di un meteoroide sia proporzionale all’impulso acquisito dal getto d’aria investito. La massa d’aria che investe un’area generica S, definita dalla proiezione della sezione d’urto del meteoroide lungo la propria traiettoria, alla velocità v in un tempo dt è Sρvdt. Così otteniamo l’equazione:

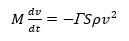
dove Γ è il coefficiente di frenamento, che esprime la porzione di quantità di moto del getto incontrato convertita in decelerazione del corpo. Il coefficiente Γ può essere sia maggiore che minore di uno. Nel caso di Γ < 1 il trasferimento di momento al meteoroide è incompleto (per esempio, il caso in cui alcune delle molecole che vengono a contatto con esso gli fluiscono attorno); l’altro caso si verifica quando diventa apprezzabile il momento relativo al rimbalzo delle molecole dalla superficie del meteoroide o alla vaporizzazione delle molecole dal meteoroide stesso.

Allo stesso tempo i meteoroidi sono soggetti ad un processo di perdita di massa, definito processo di ablazione, caratterizzato da vaporizzazione, fusione e frammentazione. In primo luogo ciò che avviene è  l’espulsione diretta degli atomi dalla superficie del meteoroide in seguito a collisione. Ognuno di tali urti libera un’energia dell’ordine di 100 eV. Mano a mano che il corpo cosmico procede nel suo tragitto si forma, vicino alla superficie, uno scudo di gas che tende a ridurre l’importanza del processo di espulsione diretta. Le molecole che ora giungono a colpire la superficie del meteoroide sono state smorzate dallo scudo di gas, per cui non hanno più energia sufficiente a espellere gli atomi del corpo cosmico. Tuttavia, riescono a riscaldarlo e ben presto si raggiungono temperature tali da fare evaporare gli atomi. Questo fenomeno è descritto dalla seconda equazione fondamentale della teoria, l’equazione di perdita di massa, che segue dall’ipotesi che una certa porzione di energia cinetica ½ Sρv³ del getto opposto di molecole è spesa in ablazione della massa dM nel tempo dt. Se Q è il calore latente di vaporizzazione o fusione del materiale che costituisce il meteoroide in unità di energia, allora l’equazione di perdita di massa si scrive come:

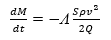
Il coefficiente Λ di trasferimento di calore descrive il consumo di energia ed è minore o uguale a uno poiché l’energia spesa nel processo di ablazione non può superare la totale energia cinetica del getto opposto di molecole. Se viene considerata anche la frammentazione, deve essere presa in considerazione la porzione di energia spesa nel processo stesso (vale a dire nel rompere i legami meccanici tra le particelle) e quella portata via dalle particelle frammentatesi.

Ablazione e decelerazione si influenzano vicendevolmente, poiché l’ablazione dipende dalla velocità del corpo mentre la decelerazione dipende dalla massa. Quindi le equazioni di perdita di massa e di frenamento per un meteoroide devono essere risolte simultaneamente.

Fatta eccezione per l’energia spesa nel processo di perdita di massa, parte dell’energia delle molecole che vengono a contatto con il bersaglio cosmico è spesa nel surriscaldare il meteoroide stesso e parte convertita in radiazione, mediante ionizzazione di atomi e molecole sia del meteoroide che dell’aria, ma la quantità più rilevante è dissipata dalle molecole d’aria e di vapore e dagli atomi considerati. La radiazione luminosa risultante si può esprimere attraverso la terza equazione fondamentale della teoria, l’equazione di luminosità, assumendo che l’intensità di radiazione I della meteora sia proporzionale all’energia cinetica della massa dM evaporata nel tempo dt:

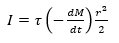
dove τ è il coefficiente di efficienza radiativo o, più comunemente, coefficiente di luminosità, che può dipendere, in generale, dalla velocità, dalla massa e dalla composizione del meteoroide.

Atomi e molecole atmosferiche e meteoriche si eccitano e ionizzano durante le collisioni anelastiche fra atomi vaporizzati del meteoroide ed atomi e molecole d’aria. Di conseguenza, lungo il tragitto della meteora si forma una scia ionizzata, o più precisamente una traccia di ioni-elettroni, in quanto ne fanno parte entrambi rendendo la scia di plasma elettricamente quasi neutra. Tale traccia assomiglia ad una colonna cilindrica molto lunga e stretta, dove le dimensioni del raggio iniziale sono circa pari al cammino libero medio a quella quota, mentre la lunghezza può arrivare a parecchi chilometri. La caratteristica più importante della scia di plasma formatasi è la densità elettronica lineare q, vale a dire il numero di elettroni per unità di lunghezza costituitisi durante il cammino della meteora. Questo parametro è descritto dalla quarta equazione, l’equazione di ionizzazione meteorica, che, se β è il numero medio di elettroni liberi formati in collisioni con altre particelle da parte di un atomo meteorico (coefficiente di ionizzazione), si può scrivere:

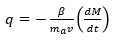
dove m_a è la massa media di un atomo meteorico.

È interessante evidenziare che sia l’intensità di radiazione I della meteora sia la densità elettronica lineare q della traccia sono proporzionali al tasso di vaporizzazione.