Forze agenti sul meteoroide dopo l’eiezione

Per capire come si distribuisce la materia nel Sistema Solare è interessante analizzare le forze che intervengono nella dinamica dei meteoroidi. Immediatamente dopo l’eiezione, l’orbita iniziale vista nel paragrafo precedente è modificata da numerose forze. In totale, la forza agente su un meteoroide di circa 10^-5 g o maggiore dopo l’eiezione è data da:

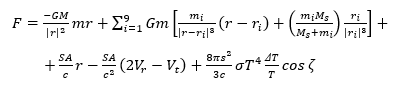
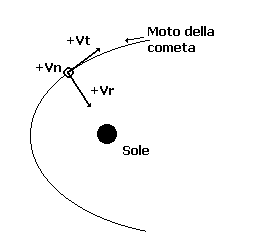
dove la somma è su tutti i pianeti da Mercurio a Plutone, r il raggio vettore dal Sole al meteoroide in UA, r_i e m_i sono il raggio vettore e la massa del pianeta i-esimo, M_s la massa del Sole, m quella del meteoroide, S è il flusso solare alla distanza r dal Sole e vale S = 1.37/r² in unità di kW m^-2, A è l’area della sezione d’urto del meteoroide relativa alla direzione solare, c la velocità della luce, V_r e V_t sono rispettivamente la velocità eliocentrica radiale e trasversale del meteoroide, s è il raggio fisico del meteoroide, σ la costante di Stefan-Boltzmann, T è la temperatura media del meteoroide, ΔT è la differenza di temperatura tra le due facce del meteoroide e ζ l’obliquità dell’asse di rotazione del meteoroide relativa alla direzione normale dell’orbita.

L’equazione precedente è composta di sei termini, ognuno dei quali rappresenta una forza fisica ben distinta agente sul meteoroide, la cui importanza relativa diminuisce procedendo da sinistra a destra.

Il primo termine rappresenta l’attrazione radiale del Sole ed è di gran lunga la forza più forte agente sul meteoroide. Il moto del corpo è definito in termini eliocentrici, così il moto è eccellentemente approssimabile ad un sistema a due corpi, Sole-meteoroide.

Il secondo termine consiste in una somma della attrazione gravitazionale diretta di ognuno dei pianeti. I termini specifici dipendono dall’estensione dell’orbita del meteoroide, ma tipicamente Giove e/o Saturno dominano.

Il terzo termine è spesso riferito a perturbazioni planetarie indirette o al termine di correzione del baricentro. Questa forza è l’analogo della forza centrifuga in un moto circolare uniforme ed è dovuta puramente ad una scelta di un sistema di coordinate non inerziali. Fisicamente, il meteoroide non si muove intorno al Sole, ma piuttosto intorno al centro di massa del Sistema Solare. Questo punto, chiamato baricentro, è lievemente spostato dal centro del Sole, a causa, in primo luogo, dell’attrazione di Giove e, secondariamente, da quella di Saturno. Esso si muove rispetto al centro solare dipendendo dalla posizione dei pianeti maggiori. Come risultato, gli elementi orbitali eliocentrici sembrano oscillare in relazione diretta all’accelerazione del baricentro relativa al centro del Sole. Questa forza diventa maggiormente significante per oggetti con orbite estremamente eccentriche vicino all’afelio, dato che la forza è dipendente dalla distanza del meteoroide dal Sole e dunque presenta un effetto maggiore quando l’oggetto è più lontano da tale stella e, cioè, quando ha l’energia potenziale più alta. L’importanza relativa di questo effetto diminuisce quando l’oggetto si muove verso l’interno del sistema e diventa pressoché insignificante quando l’oggetto è all’interno dell’orbita di Giove. Le perturbazioni indirette sono dunque tipicamente più piccole degli effetti delle perturbazioni dirette a distanza di 1-2 UA dai pianeti maggiori. Chambers ha discusso il ruolo di perturbazioni indirette nel mantenere un comportamento risonante nelle orbite delle comete di tipo Halley.

Il quarto termine dell’equazione (2.13) è dovuto alla pressione di radiazione solare. I fotoni provenienti dal Sole trasportano con loro un momento. Quando il meteoroide assorbe i fotoni solari incidenti, rimuove il momento da tale fascio di particelle. Questa variazione nel momento del fascio, cioè una forza, dal punto di vista del meteoroide, agisce sul corpo in proporzione diretta all’area della superficie geometrica esposta e alla sua efficienza scatteratrice. Per una particella perfettamente assorbente, l’efficienza scatteratrice vale uno e generalmente è il valore che viene utilizzato nei calcoli. La forza agisce radialmente in direzione opposta al Sole dato che il momento del fotone assume virtualmente tale direzione e tende a spingere la materia ai confini del Sistema Solare.

Dato che tale forza radiale decresce come 1/r², come l’attrazione gravitazionale centrale del Sole, è spesso inclusa con il termine di forza centrale. Più specificatamente, è normale riferirsi al rapporto tra forza di radiazione e di gravità come β = F_r/F_g o β = 5.7 x 10^-6/ρs, dove ρ è la densità di massa del meteoroide e s il raggio in metri. In tale maniera è possibile considerare insieme la forza di radiazione e di gravità come:

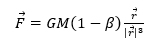
che rivela chiaramente che l’effetto della pressione di radiazione è equivalente a una diminuzione della forza centrale, che può essere causata ad esempio da un’effettiva diminuzione della massa solare. La pressione di radiazione, cioè la forza radiativa dominante per i meteoroidi che andremo ad indagare, agisce immediatamente dopo l’eiezione. Per tale motivo finché il meteoroide mantiene la sua velocità, è facile mostrare, partendo da considerazioni energetiche, che un’orbita legata prima dell’eiezione, può diventare successivamente slegata a causa dell’anomalia vera θ se la condizione:

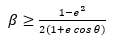
è verificata. Così, il valore di β che è richiesto ad un’orbita molto eccentrica, cioè con e tendente a 1, per diventare slegata è abbastanza basso, molto meno di uno. Per eiezioni che avvengono al perielio, quando cioè il meteoroide e il corpo progenitore si muovono alla loro maggior velocità relativa al Sole e l’energia del corpo è principalmente quella cinetica,un meteoroide delle Orionidi o Eta-Aquaridi è slegato per β > 0.01, mentre per uno delle Liridi il valore è solo β > 0.1.

Il quinto termine è dovuto all’emissione di radiazione del meteoroide. Quando la radiazione investe il meteoroide, essa è riemessa isotropicamente. Tuttavia, dato che il meteoroide si muove ad una velocità non nulla rispetto al Sole, la radiazione emessa in direzione del moto è spostata per effetto Doppler verso il blu relativamente alla radiazione emessa in direzione opposta al moto. Come risultato, la forza comunicata alla particella dalla luce spostata verso il blu, che ha un momento maggiore di quella spostata verso il rosso, agisce in direzione opposto al vettore velocità istantanea, e agisce frenando la particella. Questa forza è chiamata effetto Poynting-Robertson.

Dall’equazione emerge chiaramente che l’effetto Poynting-Robertson è dell’ordine di v/c, tipicamente circa 10^-4, relativamente alla pressione di radiazione. Per tale motivo risulta trascurabile per quanto riguarda la dinamica di particelle nel caso di brevi intervalli di tempo o per i meteoroidi più grandi. L’effetto Poynting-Robertson diventa rilevante solamente per lunghi intervalli di tempo, rimuovendo il momento e l’energia da i piccoli meteoroidi, dell’ordine del micron, in modo tale che l’orbita si circolarizza e il semiasse maggiore diminuisce, permettendo alle particelle di muoversi all’interno di regimi dove altri effetti dinamici, come le risonanze planetarie, possono avere effetto.

L’ultimo termine dell’equazione è il più difficile da misurare fisicamente e la sua importanza relativa è stata discussa per molto tempo. Tale forza risulta generata dall’asimmetria nella reirradiazione dell’energia termica assorbita da parte di un corpo rotante esposto alla radiazione solare. La parte più calda dell’oggetto cosmico irradia maggiore energia rispetto alla parte più fredda. A seconda dell’orientazione dell’asse di rotazione e del senso di spin, lo squilibrio dell’emissione di radiazione può indurre una forza, che agisce sul meteoroide in una particolare direzione. Come risultato, a differenza della pressione di radiazione o dell’effetto Poynting-Robertson, questa forza, chiamata effetto Yarkovsky-Radzievskii, è diffusa in natura e porta ad un cammino casuale nel moto perturbato del meteoroide. La direzione nella quale la forza agisce dipende dall’orientazione dell’asse di rotazione. Nessuna di queste quantità è conosciuta con un grado elevato di precisione per meteoroidi tipici. Come risultato, è possibile che nei casi estremi di oggetti rotanti lentamente, la forza esercitata dall’effetto Yarkovsky possa essere 10³-10⁴ volte rispetto alla forza prodotta dall’effetto Poynting-Robertson. Tuttavia la direzione casuale della forza nell’effetto Yarkovsky attenua il suo ruolo rispetto alla forza più piccola ma unidirezionale dell’effetto Poynting-Robertson. L’effetto Yarkovsky è ancora solamente una frazione percentuale della pressione di radiazione per un meteoroide delle dimensioni studiate in questo lavoro. Tale effetto diventa importante per lunghi periodi e per corpi molto grandi. Tuttavia, a seconda delle dimensioni e delle masse delle particelle che compongono la materia interplanetaria, i rapporti tra questi tipi di forze possono variare, contribuendo così alla distribuzione dei meteoroidi all’interno del Sistema Solare. L’effetto Poynting-Robertson è importante per particelle di dimensioni che vanno da circa un millesimo di millimetro fino a qualche centimetro, mentre per corpi di dimensioni tra 0.1 e 100 metri è invece l’effetto Yarkovsky a diventare predominante.

L’azione di queste forze è determinante nel descrivere l’evoluzione degli sciami meteorici in relazione alla vita dei loro corpi progenitori. Si possono evidenziare quattro stadi che rappresentano momenti diversi nell’evoluzione degli sciami:

il primo è caratterizzato da una breve attività, che ha un andamento asimmetrico rispetto alla posizione del corpo progenitore (come, per esempio, le Draconidi e le Leonidi);
nel secondo, la corrente delle particelle si estende lungo tutta l’orbita della cometa: la sezione del flusso è ancora ristretta e con un radiante ben definito (è il caso delle Quadrantidi e delle Perseidi);
il terzo presenta tutte le caratteristiche di un vecchio sciame omogeneo, la cui attività è meno pronunciata ed il radiante più disperso;
nel quarto stadio evolutivo, la corrente di particelle è più diffusa a causa dell’influenza, sempre maggiore, di forze dispersive ed il corpo progenitore non si comporta più come una sorgente di meteoroidi perché di quest’ultimo è rimasta ormai solo la parte più compatta del nucleo (come si presume sia il caso delle Geminidi). In quest’ultimo stadio della sua storia, lo sciame transita lentamente alla fase delle meteore a carattere sporadico e il radiante non è più localizzabile in quanto è divenuto molto disperso.

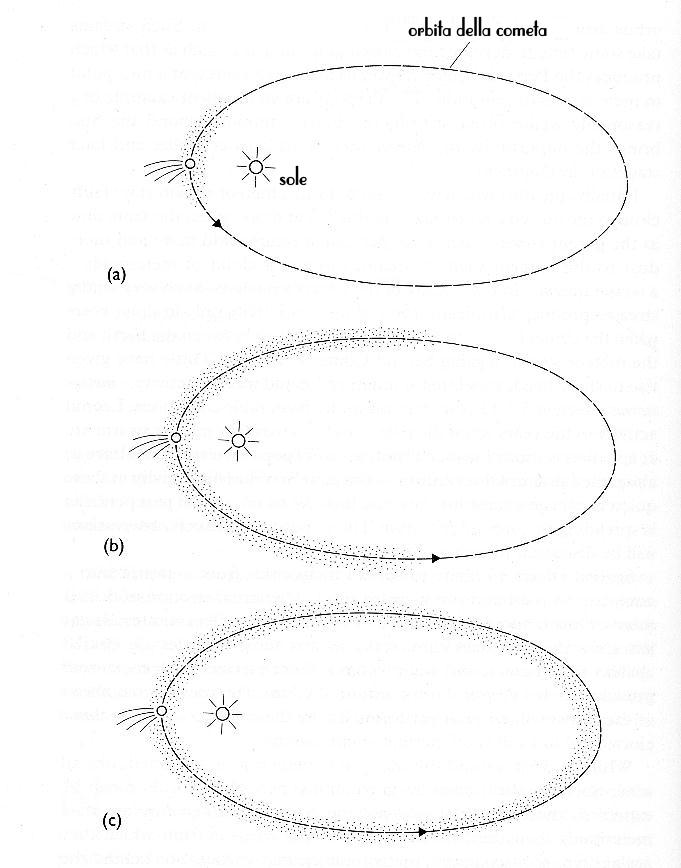
L’evoluzione nel tempo di uno sciame meteorico. Inizialmente, (a) i meteoroidi sono concentrati vicino alla cometa genitrice. Gradualmente (b) il flusso si distribuisce davanti e dietro alla cometa finché, eventualmente, i meteoroidi viaggianti con la cometa incontrano quelli precedenti ad essa e completano l’anello (c).